Bracket math: Five tips to picking your bracket based on what the numbers say

This is no easy season for picking an NCAA tournament champ. By mid-February, I usually have a gut feeling about which team I'm going to put on the final line in my bracket. In 2017 that was Kansas. But I'm also a feverish proponent of advanced metrics, and they show that the Jayhawks are a bit flawed defensively, so I'm second-guessing my gut. The advanced metrics are madly in love with Gonzaga, and while I like spending time with the Bulldogs, I'm not sure I'm ready to fully commit.
I became a Villanova believer in 2016 and am still one in 2017, but the Wildcats were saddled with the toughest region for any No. 1 seed. SI's projection system considered their No. 2 seed, Duke, to be the clear best team—not to mention one of the more talented teams of the past decade. The Blue Devils didn't look like it from November through February, but they're roaring into the tournament and making me wonder: Was the regular season just a bunch of noise?
As I was saying: This is a difficult bracket! The proper course of action here is to either fill out a pool sheet in two minutes and second-guess nothing … or study the contenders more deeply than normal. This is a five-part column for the latter. It will not lead to one, final championship answer, but it could get you closer to clarity.
Should Duke have gotten a No. 1 seed? The Blue Devils will get their say
1. Understand the profile of a champion
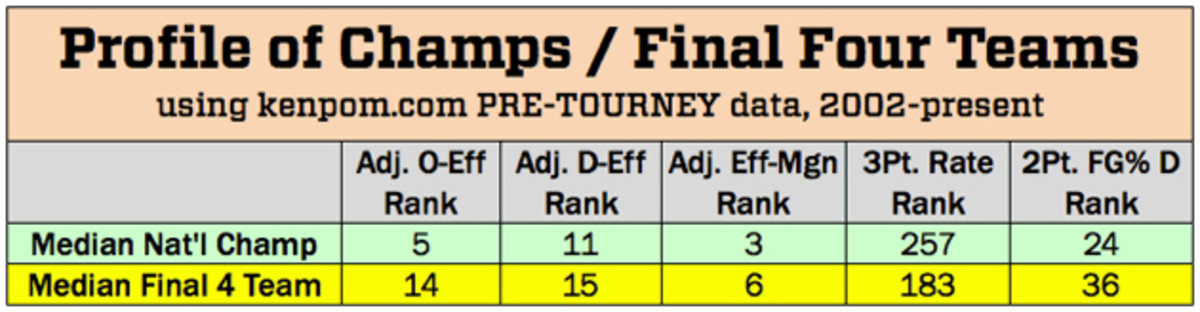
There's been a variety of NCAA tournament champs over the past 15 years, ranging from juggernauts (2009 North Carolina, 2012 Kentucky) to also-rans that went on a hot streak (2014 UConn). But knowing the median, advanced-stats profile of a title team—using 2002-present, pre-tournament data from kenpom.com—might help inform your decision.
The median rankings in the chart below are adjusted offensive and defensive efficiency (how many points a team scores per possession, adjusted for competition), overall efficiency margin, and then two non-efficiency stats that have historically mattered for champs: three-point rate (how reliant they are offensively on threes), and two-point field-goal percentage defense. For title teams, the median profile is elite offensive efficiency, pretty elite defensive efficiency, a relatively low reliance on threes and strong interior D.
2. Who fits the profile in 2017?
I took the 10 teams with the best title (gambling) odds on 5Dimes.com and analyzed their profiles using the same kenpom metrics from the previous chart. The light-green cells are where they have a close fit, the light reds are slight red flags, and the darker reds are bigger red flags.
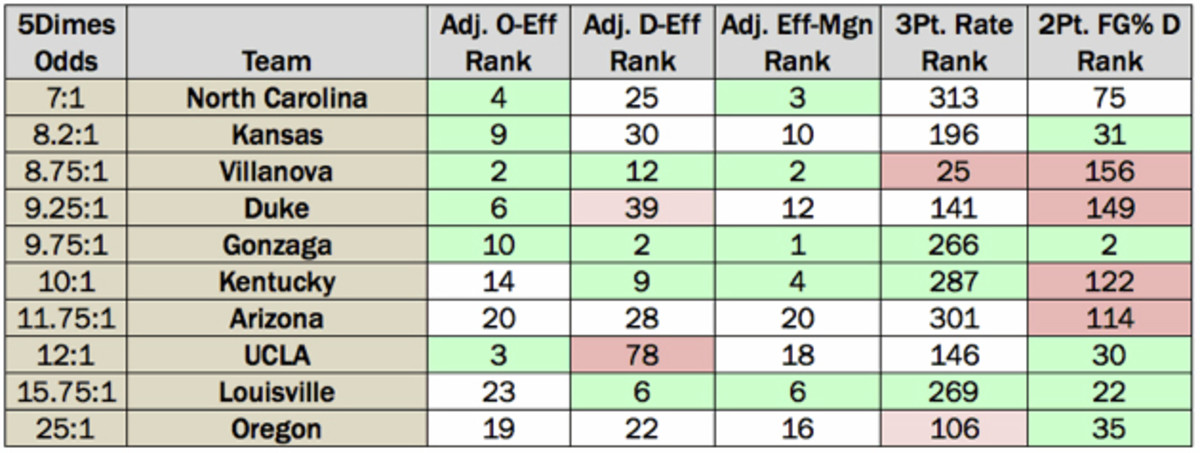
Some conclusions from this chart:
• Gonzaga is the one team that checks every box. It really does have the ideal profile of a champ, it's only lost once, and its path through the West Region isn't all that difficult. Yet, in the gambling world, the Zags only have the fifth-highest title odds. There is obvious skepticism of Gonzaga's kenpom dominance in Vegas.
• North Carolina, Kansas and Louisville all fit in at least two categories, without any red flags. If you're skeptical of Gonzaga, the Tar Heels and Jayhawks are your most logical (and safest) landing points.
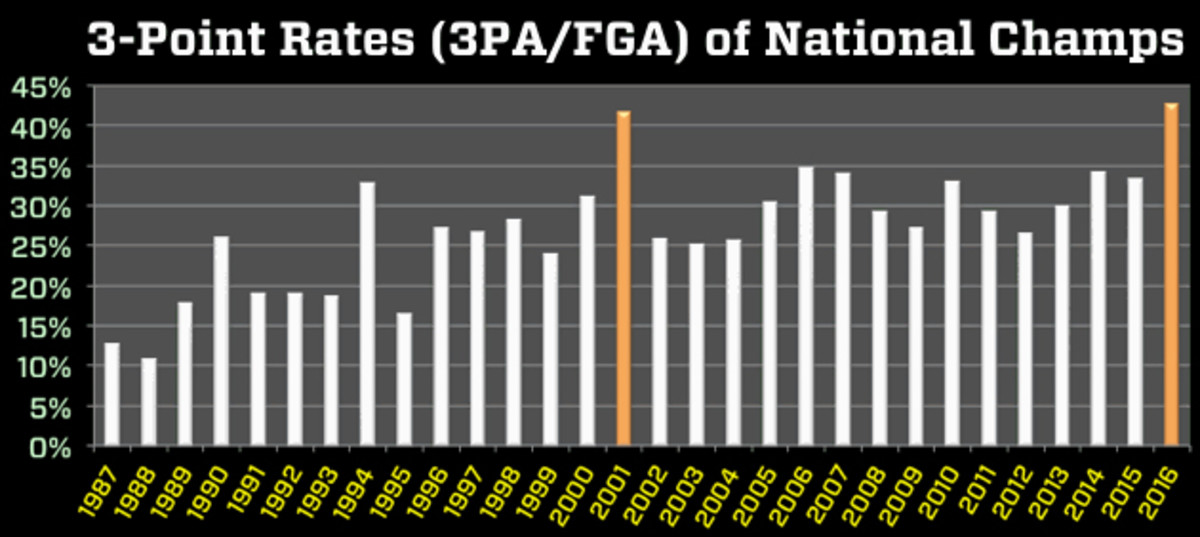
• Villanova's efficiency profile is the most champion-like of any team, but the Wildcats have two red flags: weak interior D, due to lack of size and depth, and the heaviest reliance on three-pointers of any title contender. It's not always a bad thing to be three-reliant, but higher reliance on threes makes an offense more volatile in a must-win-six-in-a-row tournament. When 'Nova won it all last year, it became just the second champ in the three-point era to take more than 40% of its shots as threes, joining 2001 Duke:
3. Who would have to defy history?
UCLA is the lone, bad defensive outlier in that contenders chart. The Bruins' offense has been amazing—I said in December that it's the most entertaining scoring attack in the nation, and that's still the case—but Steve Alford's team ranks 78th in defensive efficiency. Which would mean that, if UCLA were to make it out of the South Region, it would be the second-worst defensive team in the entire efficiency era (2002-present) to reach the Final Four. Only 2011 VCU, the most improbable Final Four team in a long, long time, is worse:
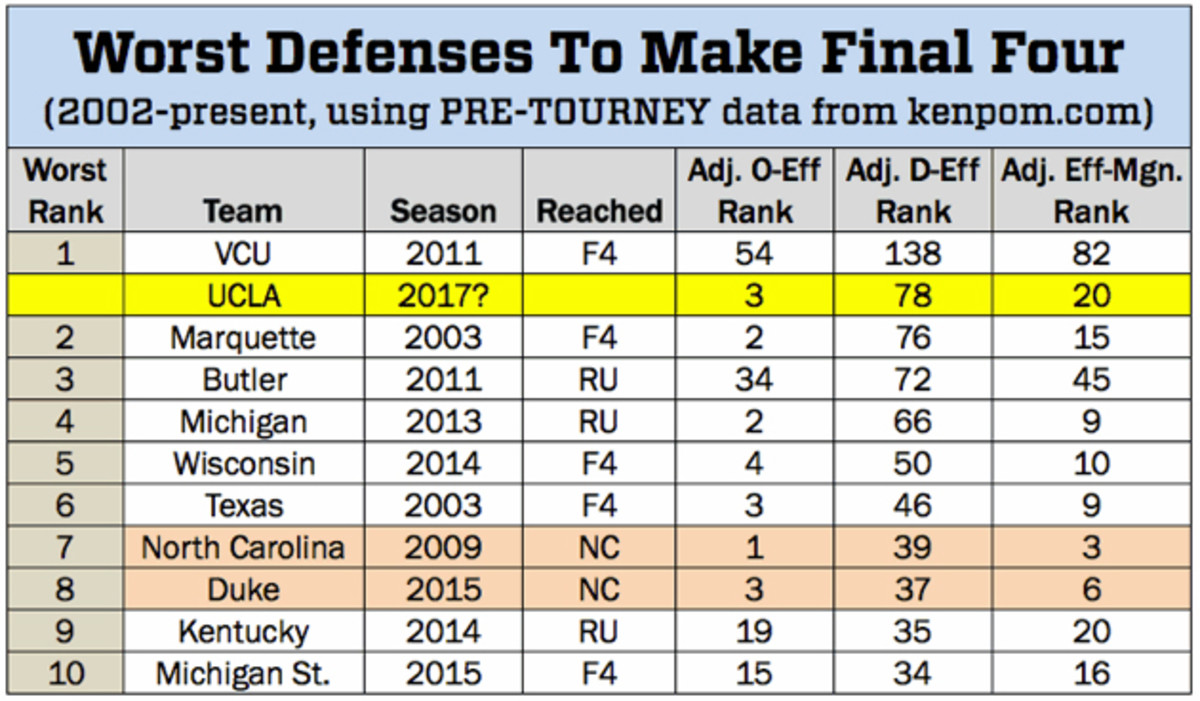
The worst pre-tournament defenses that went on to win a national title were 2009 North Carolina (39) and 2015 Duke (37), yet both were significantly better than UCLA is now. The Bruins' most successful comps are 2003 Marquette, which lost in the Final Four with a Dwyane Wade-powered, elite offense, and 2013 Michigan, which came within a few possessions of a championship.
Enter Here

Cousin Sal Bets The House
Fill out a perfect bracket, win Cousin Sal’s L.A.-area home.
4. But let's get back to Gonzaga
I couldn't recall another situation as extreme as Gonzaga's, where a title contender was so beloved by adjusted efficiency rankings and not by Vegas or the general, bracket-picking populace. (In ESPN's bracket challenge, the Zags are the seventh-most popular title pick.) Could kenpom just be an outlier that's significantly overvaluing them?
For another perspective—and with invaluable assistance from Pythagorean-converter Seth Burn (@SethBurn)—I created a composite metric. It averages the Pythagorean winning percentages from six ranking systems (kenpom, ESPN's BPI, Sagarin, Massey, Matchup Zone and Dolphin) and one preseason projection system (SI's model, from Dan Hanner and myself, to serve as a talent-and-coaching hedge against regular-season noise). In this composite, Villanova comes out No. 1, but Gonzaga is still a very close second, and Duke leaps up into the top four:
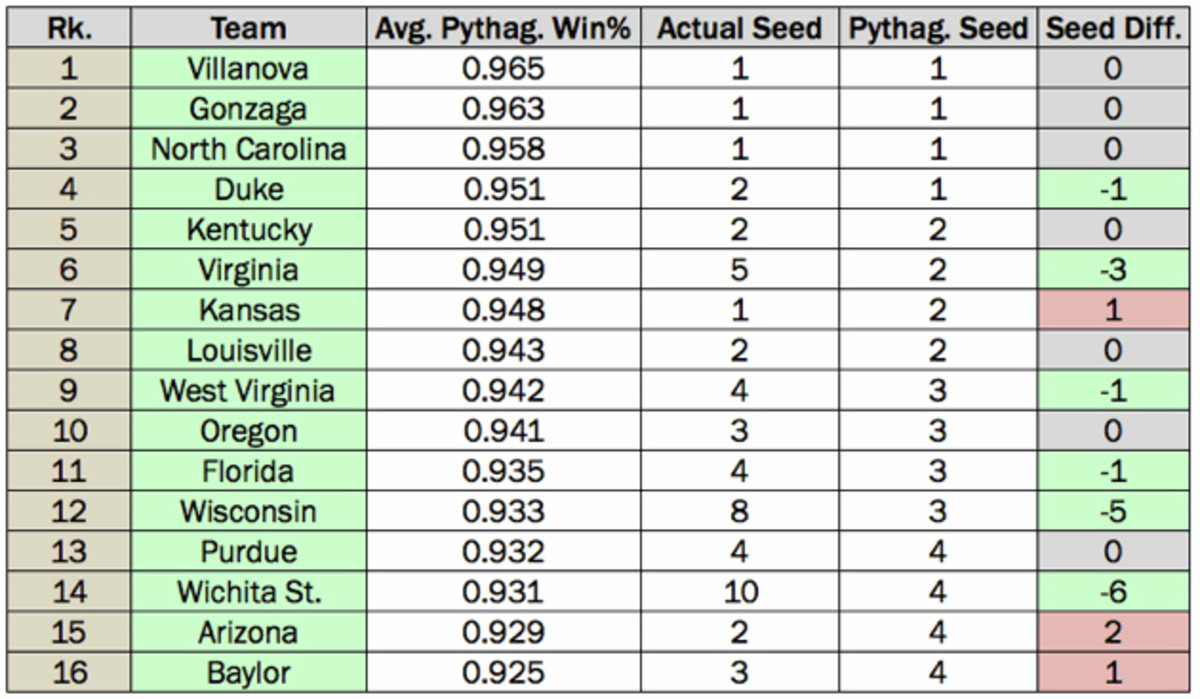
The bad news for Villanova is that this composite metric believes the East Region has the most difficult No. 2 seed (Duke), the second-most difficult No. 3 (Baylor), the second-most difficult No. 4 (Florida) and the most difficult No. 5 (Virginia). Gonzaga, with a weak West Region, has much better odds than 'Nova does of getting to the Final Four.
5. Applying the composite to regions
John Ezekowitz (@JohnEzekowitz) provided some crucial assistance by using the composite metric to run Log5 odds on each region. The results gave us a better idea of what contenders have the easiest or toughest paths to Phoenix.
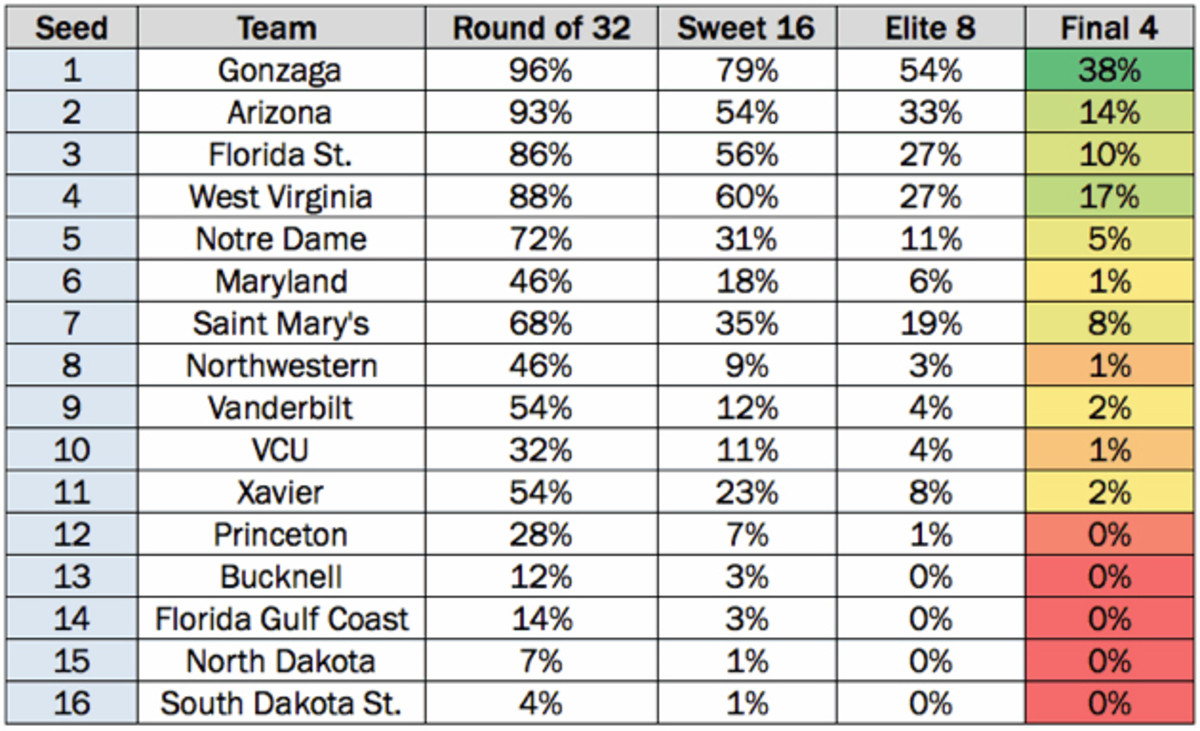
Let's start with the West, where Gonzaga has the highest Final Four odds in the entire field (38.0%), and the No. 4 seed, West Virginia, has the second-highest Final Four odds in the region:
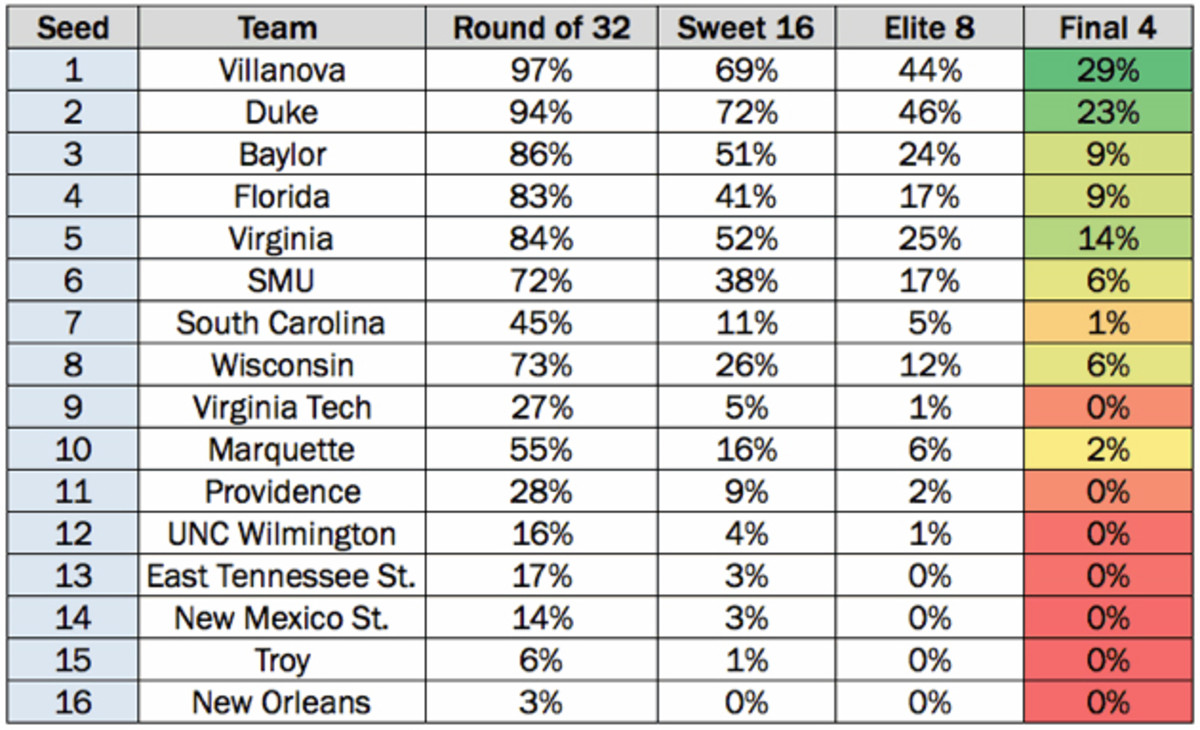
In the East, as I already mentioned, 'Nova's odds are depressed by its company, as even the No. 6 (SMU) and No. 8 (Wisconsin) seeds are an outside threat to make the Final Four:
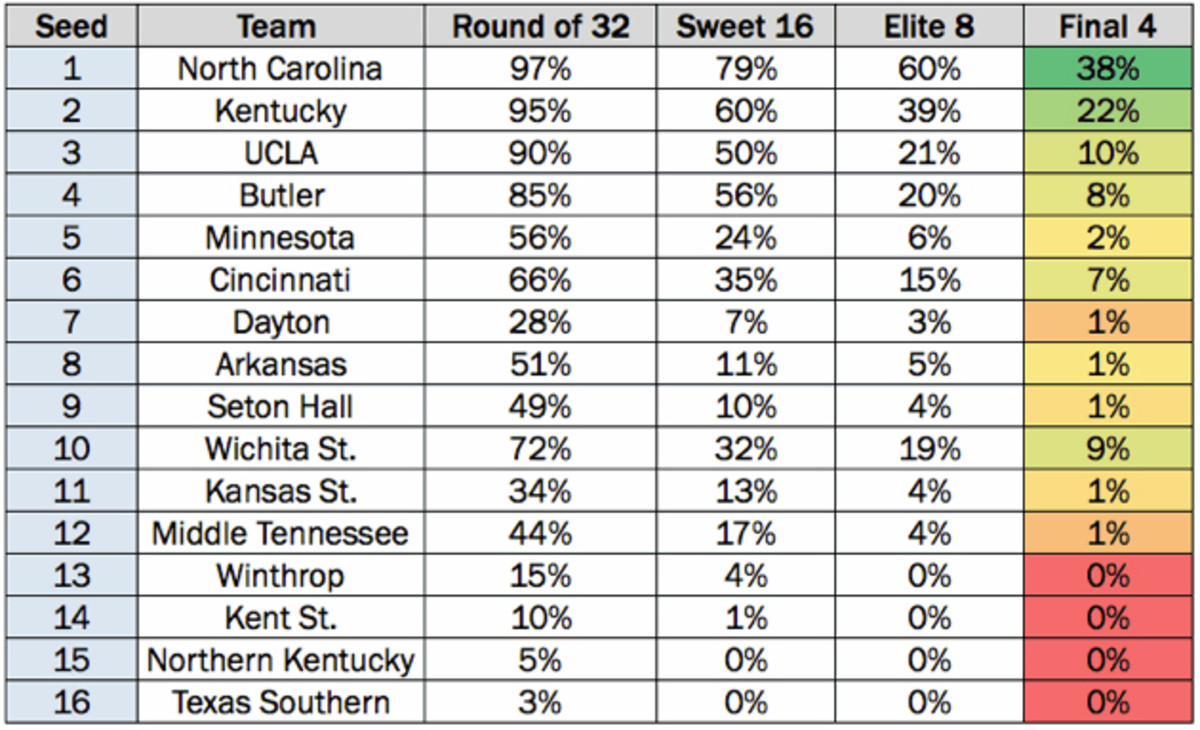
Moving on to the South: North Carolina has the second-highest Final Four odds (37.5%) in the entire field, in part because the 4–9 lines are perceived to be so weak, and one of the four strongest teams (Kentucky or Wichita State) will get knocked out in the second round.
In the Midwest, Kansas has the lowest Final Four odds of any No. 1 seed in the entire bracket. The composite metric doesn't love the Jayhawks, ranking them seventh overall, and the presence of a strong 2–3 combo, including a Louisville team that's viewed as almost Kansas' equal, brings down KU's odds.
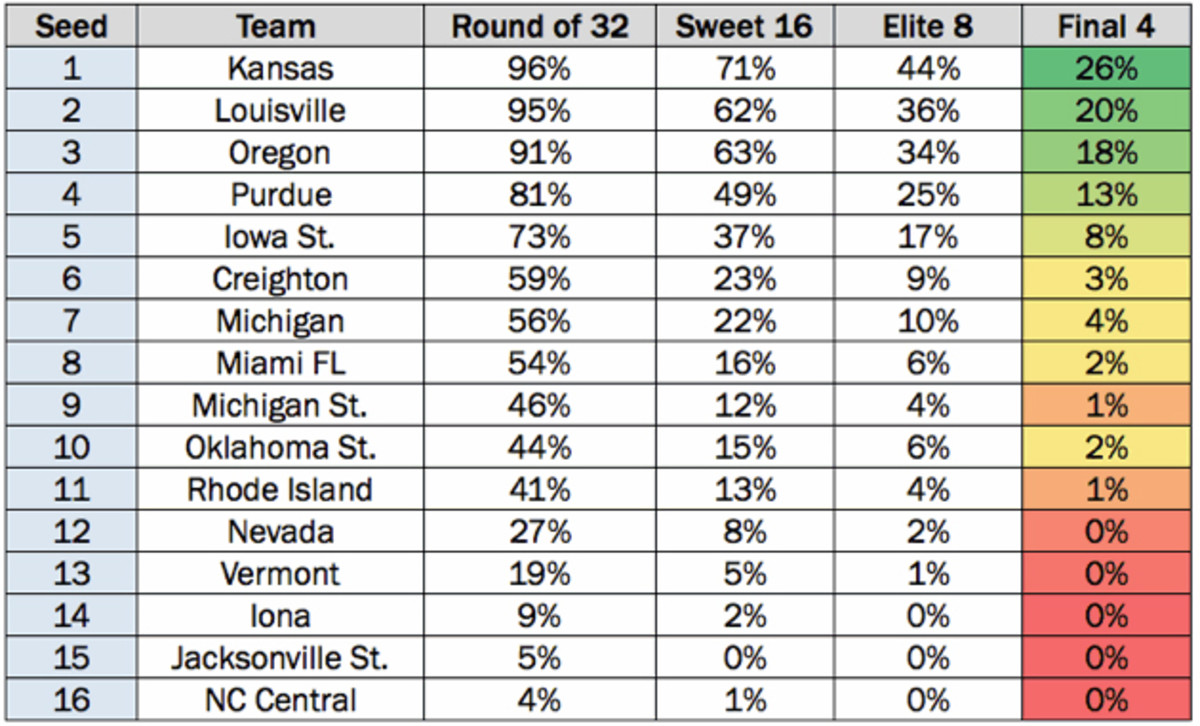
It's understandable, after running these numbers, that Vegas has settled on North Carolina as a favorite; the Tar Heels and Gonzaga have by far the best Final Four odds, and UNC's metrics are backed by major-conference results that bettors trust.
Your bracket either comes down to what data you believe in—efficiency says Gonzaga; the composite ranking's odds say Gonzaga or North Carolina; the pure composite ranking says Villanova; betting markets say Carolina; preseason polls and projections said Duke—or a belief that in a title race this muddled, you have to narrow it down and then go with your gut.
