Louisville, Florida final two standing in second annual Survival Bracket

This is Year 2 of an experiment we call the Survival Bracket. It applies a statistical method used in clinical drug trials -- called "survival analysis" -- to assess teams' risk of falling out of the bracket at each stage. Its strength is the later rounds, and last year's Survival Bracket did quite well, picking seven Elite Eight teams, three Final Four teams and the correct champ. When John created the model, he also retroactively applied it to the 2007-2011 tournaments, and over the past six seasons its predictions have outperformed the RPI and kenpom.com's efficiency rankings:

The survival model treats the NCAA tournament as a unique setting rather than just a series of matchups that might've taken place in the regular season. It doesn't ignore efficiency: it uses kenpom.com's adjusted offensive and defensive efficiencies and strength-of-schedule ratings as the "control" variables for its initial 1-68 rankings. The survival model then makes adjustments based on data that John found to have a correlation to NCAA tournament success. The four significant factors are:

* Consistency: how little a team's efficiency margin varies from game-to-game.

* Experience -- and especially tourney experience: a team's returning minute percentage multiplied by the number of NCAA tournament games in which it appeared last season.

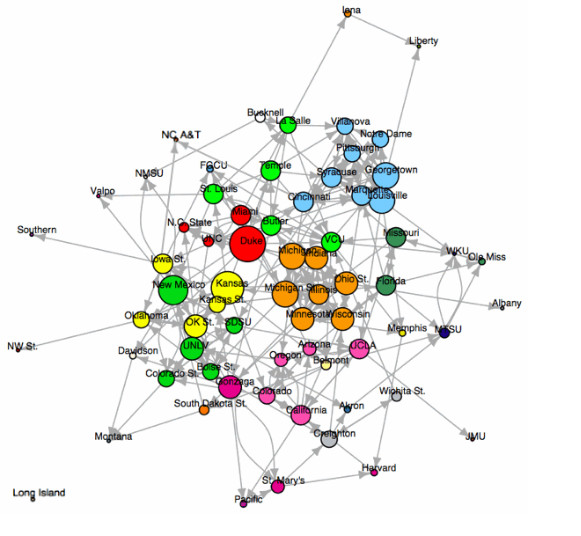
* Out-Degree Network Centrality: The model builds an amazing matrix of where all 68 tourney teams' schedules intersected.

The number of games played against NCAA tournament teams (network centrality) and the number of games won against NCAA tournament teams (the out degree, or arrows running away from a network node) were significant. Different values were assigned to home, road and neutral wins within the network. (There's just one "isolate," or team that didn't face a single opponent from the NCAA tournament field all season. That's No. 16 Long Island. In the six-year testing sample, isolates failed to win a single NCAA tournament game. The consistent teams that are major hubs of connectivity -- Duke, for example -- have the lowest risk of early failure.)

* The negative interaction of the Experience and Out-Degree Centrality variables. They get multiplied together to account for declining returns, so the model doesn't overestimate a team with a ton of experience and games against NCAA tournament teams.

A Cox Proportional Hazards regression was applied to this data in order to re-rank teams 1-68, based on their relative risk of failure. We then used these rankings to fill out the 2013 Survival Bracket.

In the Round of 64, the model favored two double-digit seeds: No. 11 Minnesota (over UCLA) and No. 11 Bucknell (over Butler). Our rule was also to pick double-digit upsets that had a 48 percent confidence or higher and a high-variance (meaning inconsistent) opponent, and that led to No. 11s Middle Tennessee State or St. Mary's both being picked over Memphis. The highest-variance team in the Round of 32, Michigan, was also knocked out in favor of slight underdog VCU.

Two noteworthy things that did not reach the level of actual bracket picks: Bucknell has the best odds of any double-digit seed of surviving to the Sweet 16 (24.8 percent) or Elite Eight (11.6 percent). And among the 14-15-16 seeds, Davidson has the best odds, by far, of pulling off an upset in its first game (42.7 percent).

Overall, the bracket is rather chalky, because the model did not love any 2-3-4 seeds other than Florida. The Gators, its national title pick, had a lot factors working in their favor: they ranked No. 1 in efficiency, they returned the majority of an Elite Eight rotation, and they were reasonably well-connected in the network, with seven tourney teams.

The model says the Florida-Louisville title game is essentially a coin-flip, with the Gators holding a 51.5 percent chance of survival. The Cardinals have strong efficiency ratings, Final Four experience and network centrality, but the Survival Bracket went with Florida because its ceiling was higher. When the Gators play at their peak level -- even though that didn't happen in recent SEC games -- they're the best team in the country. The model thinks they're similar to the 2007 Joakim Noah-led Gators, who were inconsistent during the regular season, but had the highest ceiling of anyone in the bracket. That version of Florida woke up just in time for the tourney, and you're well aware of what happened next.